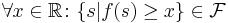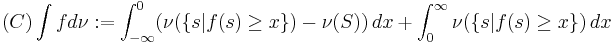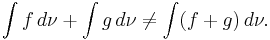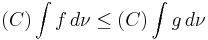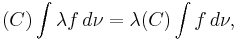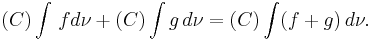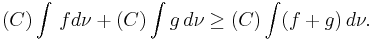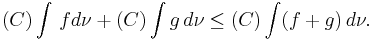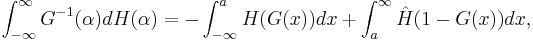Choquet integral
In decision theory, a Choquet integral is a way of measuring the expected utility of an uncertain event. It is applied specifically to membership functions and capacities. In imprecise probability theory, the Choquet integral is also used to calculate the lower expectation induced by a 2-monotone lower probability, or the upper expectation induced by a 2-alternating upper probability. This integral was created by the French mathematician Gustave Choquet.
Using the Choquet integral to denote the expected utility of belief functions measured with capacities is a way to reconcile the Ellsberg paradox and the Allais paradox[1].
Contents |
Definition
More specifically, let  be a set, and let
be a set, and let 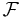 be any collection of subsets of
be any collection of subsets of  . Consider a function
. Consider a function 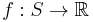 and a monotone set function
and a monotone set function 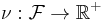 .
.
Assume that  is measurable with respect to
is measurable with respect to  , that is
, that is
Then the Choquet integral of  with respect to
with respect to  is defined by:
is defined by:
where the integrals on the right-hand side are the usual Riemann integral (the integrands are integrable because they are monotone in  ).
).
Properties
In general the Choquet integral does not satisfy additivity. More specifically, if  is not a probability measure, it may hold that
is not a probability measure, it may hold that
for some functions  and
and  .
.
The Choquet integral does satisfy the following properties.
Monotonicity
If 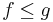 then
then
Positive homogeneity
For all 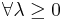 it holds that
it holds that
Comonotone additivity
If 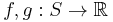 are comonotone functions, that is, if for all
are comonotone functions, that is, if for all 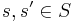 it holds that
it holds that
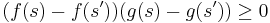 .
.
then
Subadditivity
If  is 2-alternating, then
is 2-alternating, then
Superadditivity
If  is 2-monotone, then
is 2-monotone, then
Alternative Representation
Let  denote a cumulative distribution function such that
denote a cumulative distribution function such that 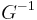 is
is 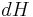 integrable. Then this following formula is often referred to as Choquet Integral:
integrable. Then this following formula is often referred to as Choquet Integral:
where 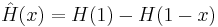 .
.
- choose
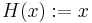 to get
to get ![\int_0^1 G^{-1}(x)dx = E[X]](/2012-wikipedia_en_all_nopic_01_2012/I/bfebd2a4376b087c31dbac6106e2e8ec.png) ,
, - choose
![H(x):=1_{[\alpha,x]}](/2012-wikipedia_en_all_nopic_01_2012/I/ba67a9ece88120d6024ba086e5ed6058.png) to get
to get 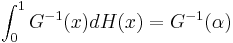
Notes
- ^ Chateauneuf A., Cohen M. D., "Cardinal extensions of EU model based on the Choquet integral", Document de Travail du Centre d’Economie de la Sorbonne n° 2008.87
External links
- Gilboa I., Schmeidler D. (1992), Additive Representations of Non-Additive Measures and the Choquet Integral, Discussion Paper n° 985...